Commonly Asked Sorting Algorithms Summary

Sort

Word count: 973Reading time: 6 min

 2022/01/13 

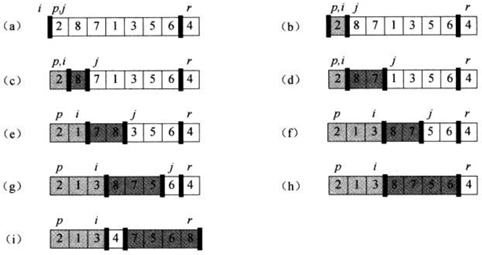
Quick Sort (Randomized)

Quicksort is a Divide and Conquer algorithm. Like all divide-and-conquer algorithms, it first divides a large array into two smaller subarrays and then recursively sort the subarrays. Basically, three steps are involved in the whole process:

Pivot Selection

Randomly (otherwise it will time out) pick an element, called pivot, from the array.

Partitioning

Reorder the array such that all elements with values less than the pivot come before the pivot. In contrast, all elements with values greater than the pivot come after it. The equal values can go either way. After this partitioning, the pivot is in its final position.

Recursion

Recursively apply the Step 1 & 2 to each subarray.

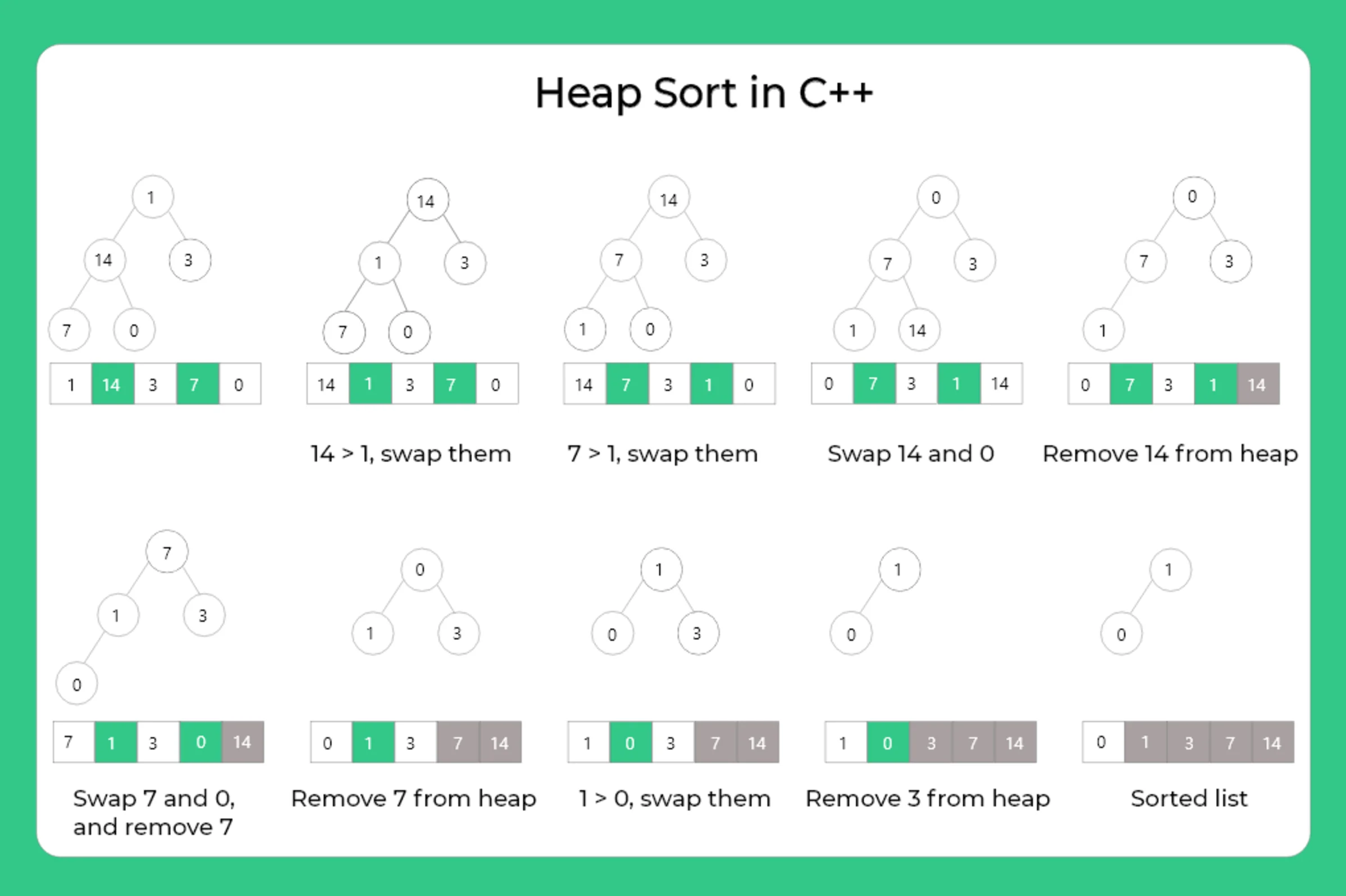
This is a picture

Code

// Quick Sort
void randomizedQuickSort(vector<int>& nums, int left, int right) {
    if (left < right) {
        int p = randomizedPartition(nums, left, right);
        randomizedQuickSort(nums, left, p - 1);
        randomizedQuickSort(nums, p + 1, right);
    }
}

int randomizedPartition(vector<int>& nums, int left, int right) {
    int randNum = (rand() % (right - left + 1)) + left; // Generate a random pivot
    swap(nums[right], nums[randNum]);
    int pivot = nums[right];
    int i = left - 1;
    for (int j = left; j < right; j++) {
        if (nums[j] <= pivot) {
            i++;
            swap(nums[i], nums[j]);
        }
    }
    swap(nums[i + 1], nums[right]);
    return i + 1;
}

Heap Sort

A heap is a complete binary tree. An ordered balanced binary tree is called a Min-heap, where the value at the root of any subtree is less than or equal to the value of either of its children. An ordered balanced binary tree is called a Max-heap, where the value at the root of any subtree is more than or equal to the value of either of its children.

To sort any list into a logical order following steps are followed :

Convert the list into heap.
Convert this heap into max heap.
Replace the root with the last item of the heap.
Delete this node and reduce the size of the heap by 1.
Repeat Step 1-4 until sorted.

This is a picture

Code

// Heap Sort
void heapify(vector<int>& nums, int n, int i) {
    int largest = i;
    int left = 2 * i + 1;   // left child
    int right = 2 * i + 2;  // right child
  
    // If left child is larger than root
    if (left < n && nums[left] > nums[largest]) {
        largest = left;
    }
  
    // If right child is largest
    if (right < n && nums[right] > nums[largest]) {
        largest = right;
    }
  
    //If root is not largest
    if (largest != i) {
        swap(nums[i], nums[largest]);
        // recursive
        heapify(nums, n, largest);
    }
}

// n is the size of nums
void heapSort(vector<int>& nums, int n) {
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(nums, n, i);
    }
  
    // One by one extract an element from heap
    for (int i = n - 1; i >= 0; i--) {
        // Move current root to end 
        swap(nums[i], nums[0]);
        // Calling max heapify on the reduced heap
        heapify(nums, i, 0);
    }
}

Bucket Sort

Calculate the number of each element in nums. Use count to store these numbers.
Traverse count. i-th element’s value is the occurrence times of the corresponding number.

Code

vector<int> bucketSort(vector<int>& nums) {
    vector<int> count(5e4 + 5e4 + 1, 0); // 5e4 + 5e4 + 1 : the range of numbers in nums (-5e4<= n <= 5e4)
    for (auto num : nums) count[num + 5e4]++; // Calculate the number of each element in nums. 
    int k = 0;
    for (int i = 0; i < count.size(); i++) {
        // count[i]-- > 0 : 1. count[i] > 0, 2. count[i]-- 3. other instructions inside the while loop.
        while(count[i]-- > 0) nums[k++] = i - 5e4;
    }
    return nums;
}

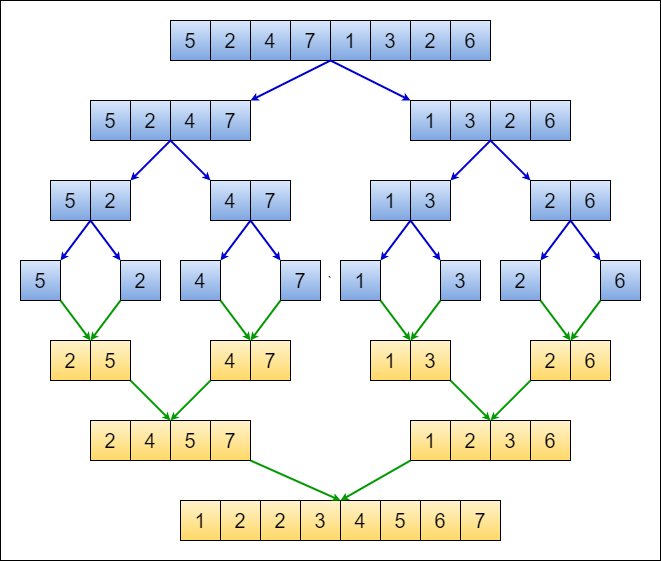
Merge Sort

Merge sort is a divide and conquer algorithm:

If it is only one element in the list it is already sorted, return.
Divide the list recursively into two halves until it can no more be divided.
Merge the smaller lists into new list in sorted order.

Ket function: merge(nums, start, end, mid)

The essence of this function is to merge 2 sorted arrays. Pointer i and j respectively point to the first position of the first half and the second half of the array nums. Then compare nums[i] and nums[j]. If nums[i] > nums[j], push nums[i] to the temporary array tmp, and i++, otherwise push nums[j] to the temporary array tmp, and j++. When one part is done, push the rest of the other part to the tmp. Finally, cover unsorted array nums by sorted tmp.

This is a picture

Code

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
    	mergeSort(nums, 0, (int)nums.size() - 1);
    	return nums;
    }

    // Divide
    void mergeSort(vector<int>& nums, int start, int end) {
    	if (start >= end) return;
    	int mid = (start + end) / 2;
    	mergeSort(nums, start, mid);
    	mergeSort(nums, mid + 1, end);
    	merge(nums, start, mid, end);
    }

    // Merge
    void merge(vector<int>& nums, int start, int mid, int end) {
        vector<int> tmp(end - start + 1);
        int i = start, j = mid + 1, k = 0;
        while (i <= mid && j <= end) {
        	if (nums[i] < nums[j]) {
                tmp[k++] = nums[i++];
            }
        	else {
                tmp[k++] = nums[j++];
            }
        }
        while (i <= mid) tmp[k++] = nums[i++];
        while (j <= end) tmp[k++] = nums[j++];
        for (int idx = 0; idx < tmp.size(); idx++) {
        	nums[start + idx] = tmp[idx];
        }
    }
};

References

Next Post

Binary Tree Traversal
Previous Post

Kadane's Algorithm